昔からどうしてもよくわからない&旨く解けない問題に二次元cavity問題の数値解法があります。
二次元 cavity 問題とは、以下のような断面の容器の中を流れる流体の流速・圧力を求める問題です。
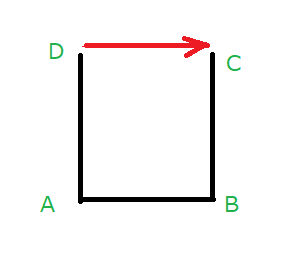
ここで、AB, BC, DA 上は粘着条件から u, v をそれぞれ点 x, y におけるX方向、Y方向の流速として、
,
一方、CD 上では速さ u0 の流速があるとして、
,
とします。ここからは流体解析Ⅰの受け売りです。計算格子として、いわいる「スタガード格子」を採用します。(u, v, p) は互い違いの、それぞれ異なる位置で定義されます。
基礎方程式となる Navier-Stokes 方程式は非圧縮とすると二階微分が出現することから正方形 ABCDの「外側」の物理量がないと計算できません。辺AB, BC, DA上では、u, v は境界上では0なので、u, v に関する時間発展の式から (V = (u, v))
辺CD上では
となるが、辺CD上では u=u0なので、辺AB, BC, DA と同じ式に帰着します。
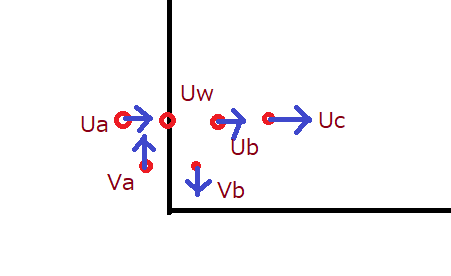
「外側」に関しては辺DAを例に考えると、u(w) = 0 なので、v(w) = 0 を考慮して、
, ,
辺CD上では u(w) = u0 なので、ua = u0 – ub とします。
MAC法では、Navier-Stokes 方程式の圧力項について、まず右辺に u,v のみを含む poisson 方程式を導出し、圧力を解いた後で u, v の時間発展を求めます。基礎方程式は以下になります。
ここまで書いたところでどっと疲れたので、続きはまたあとで。

コメントを残す