昨日に引き続き、重力計算です。昨日のアイデアを python + PyTorch で実現すると、以下のようになります。
# ライブラリのインポート
import torch
import matplotlib.pyplot as plt
import time
from matplotlib.animation import FuncAnimation
# Apple MPS チェック
device = 'cpu'
if torch.backends.mps.is_available() == True:
device = 'mps'
if torch.cuda.is_available() == True:
device = 'cuda:0'
dv = torch.device(device)
cp = torch.device('cpu')
print("Use device: ", dv)
# 初期化
n = 100
x = torch.rand(n, 2, dtype=torch.float32).to(dv)
xn = torch.zeros(n, 2, dtype=torch.float32).to(dv)
dx = torch.zeros(n, n, 2, dtype=torch.float32).to(dv)
gv = torch.zeros(n, n, 2, dtype=torch.float32).to(dv)
dxa1 = torch.zeros(n, n, dtype=torch.float32).to(dv)
dxa2 = torch.zeros(n, n, dtype=torch.float32).to(dv)
v = torch.rand(n, 2, dtype=torch.float32).to(dv)
vn = torch.zeros(n, 2, dtype=torch.float32).to(dv)
tt = 0.
lp = 0
dt = 0.001
epsilon = torch.tensor(1e-9).to(dv)
omega = torch.tensor(1e+9).to(dv)
G = torch.tensor(10.0).to(dv)
# 慣性座標系に移る
xm = torch.sum(x, dim=0)
x -= xm / n
vm = torch.sum(v, dim=0)
v -= vm / n
# 猫額空間の取得
fig, ax = plt.subplots()
# 位置情報の更新
def integral_r(frame):
xn[:, :] = x[:, :] + dt * v[:, :]
# 速度情報の更新
def integral_v(frame):
for i in range(n):
dx[i, :, :] = x[i, :] - x[:, :]
dxa = torch.abs(dx)
dxa1[:, :] = torch.min(dxa[:, :, 0] + dxa[:, :, 1] + epsilon, omega)
dxa2[:, :] = dxa[:, :, 0] - dxa[:, :, 1]
dxa2[:, :] /= dxa1[:, :]
sq = torch.sqrt(1. + dxa2 * dxa2) * dxa1 / 1.4142136
for i in range(2):
sq = 1.0 / (sq * sq * sq)
gv[:, :, 0] = dx[:, :, 0] * sq[:, :]
gv[:, :, 1] = dx[:, :, 1] * sq[:, :]
gva = G * torch.sum(gv, dim=0)
vn[:, :] = v[:, :] + dt * gva[:, :]
# フレーム処理
def next_frame(frame):
global tt, lp
ct = time.time()
plt.cla()
integral_v(frame)
integral_r(frame)
x[:, :] = xn[:, :]
v[:, :] = vn[:, :]
xp = x.to(cp)
tt = tt + dt
lp += 1
if lp % 10 == 9:
ed = time.time()
diff = ed - ct
print("t=", tt, ", elapsed=", diff)
last_tt = int(tt)
ax.plot(xp[:, 0], xp[:, 1], '.', color='blue', markersize=5)
# アニメーションの定義
anim = FuncAnimation(fig, next_frame, interval = 100, frames = 100)
# 実行
plt.show()
M3 Mac (mps あり) で計測したところ、以下のようになりました。
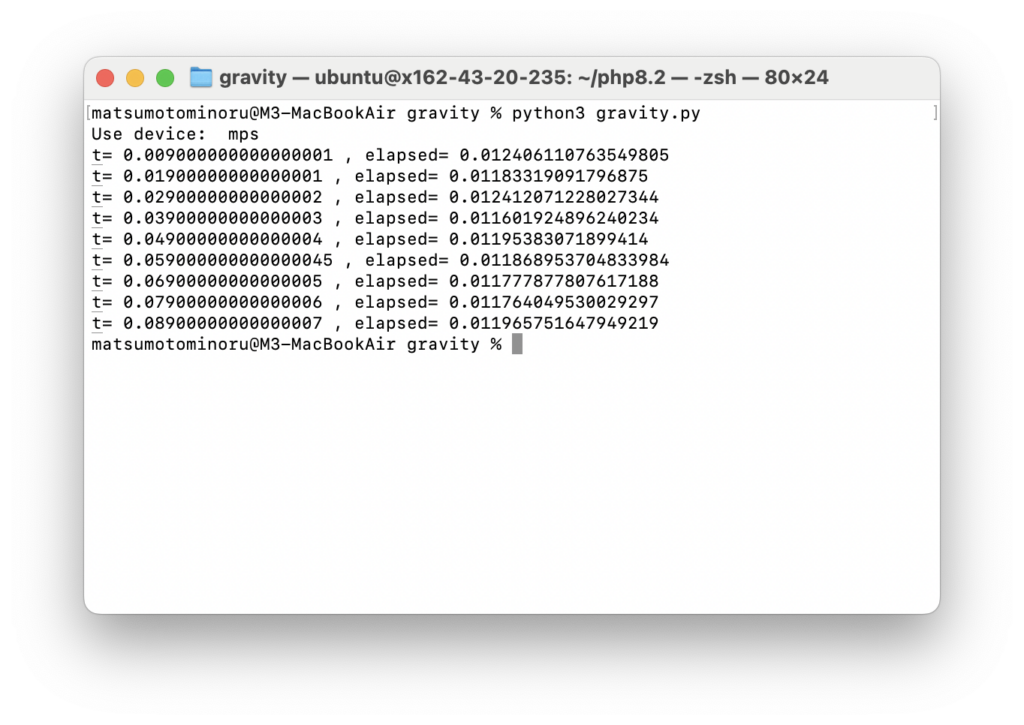
RTX 4090 (CUDA) で計測したところ、以下のようになりました。
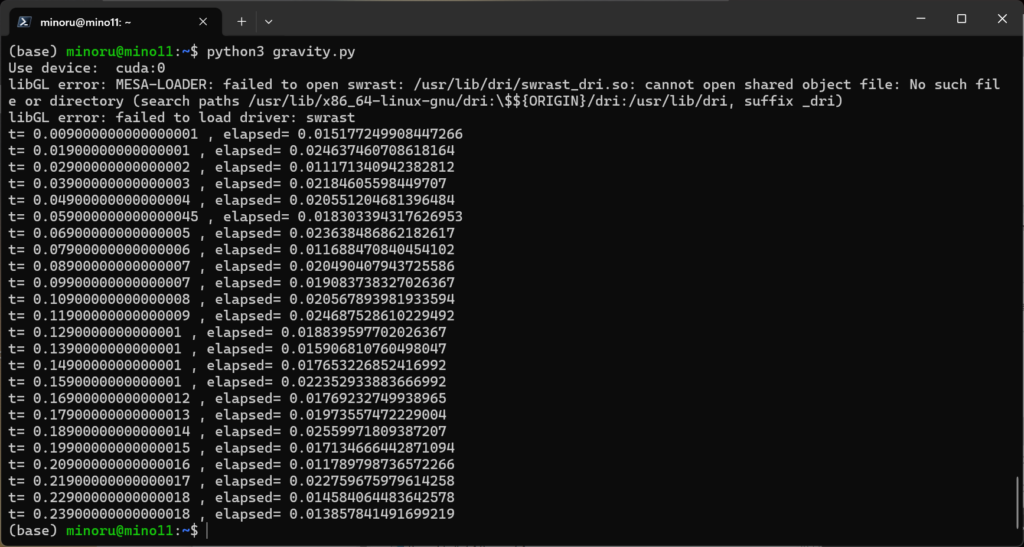
本来は RTX 4090 の方が速いはずですが、データのロードに時間がかかっているものと思われます。
実際、n=1000, 10000 などとすると、CUDA の方が速くなります。
CUDA で使用していた VRAM は 2GB でした。
消費電力を考えると、M3 よく頑張っているなという印象です。

1 throught on "重力計算再び: 続き"