二次元 cavity 問題のMAC法による数値解法(2)

前回、「スタガード格子」をさらっと通り過ぎましたが、具体的には、以下のような格子をとります。

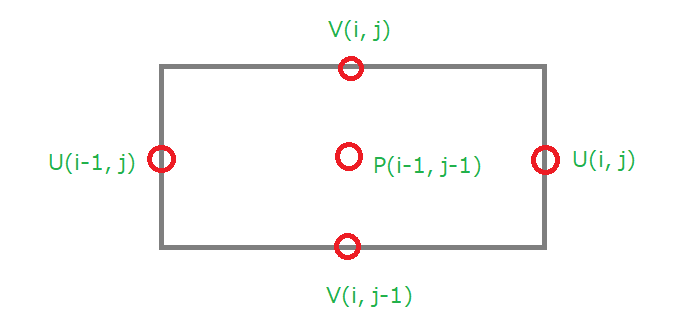
通常はある点で物理量が定義されますが、スタガード格子では各点で異なる物理量が定義されます。

例えば v(i, j) における u(i, j) の値は定義されていないため、平均をとって物理量を近似します。

${\stackrel{—}{u}}_{i,j}=\frac{u_{i+1,j+1}+u_{i+1,j}+u_{i,j+1}+u_{i,j}}{4}$, ${\stackrel{—}{v}}_{i,j}=\frac{v_{i+1,j+1}+v_{i+1,j}+v_{i,j+1}+v_{i,j}}{4}$

このことに注意して前回の方程式を中心差分で二次元に書き下すと、連続の式の微分は無視して、

$D_{i,j}=\frac{u_{i+1,j}–u_{i,j}}{d}+\frac{v_{i,j+1}–v_{i,j}}{d}$

$p_{i,j}=\frac{1}{4}\left[\right(p_{i+1,j}+p_{i–1,j}+p_{i,j+1}{p}_{i,j–1})–\frac{d^2}{\Delta t}{D}_{i,j}\mathrm{+}{(u_{i+1,j}–u_{i,j})}^2+{(v_{i,j+1}–v_{i,j})}^2+2({\stackrel{—}{u}}_{i,j}–{\stackrel{—}{u}}_{i,j–1}\left)\right({\stackrel{—}{v}}_{i,j}–{\stackrel{—}{v}}_{i–1,j}\left)\right]$

$u_{i,j}^{n+1}=u_{i,j}–\mathrm{\Delta t}\left[u_{i,j}\right(\frac{u_{i+1,j}–u_{i–1,j}}{2d})+{\stackrel{—}{v}}_{i,j}(\frac{v_{i,j+1}–v_{i,j–1}}{2d})+\frac{p_{i+1,j}–p_{i,j}}{d}–\frac{1}{Re{d}^2}(u_{i+1,j}+u_{i–1,j}+u_{i,j+1}+u_{i,j–1}–4u_{i,j}\left)\right]$

$v_{i,j}^{n+1}=v_{i,j}–\mathrm{\Delta t}\left[v_{i,j}\right(\frac{v_{i,j+1}–v_{i,j–1}}{2d})+{\stackrel{—}{u}}_{i,j}(\frac{u_{i+1,j}–u_{i–1,j}}{2d})+\frac{p_{i,j+1}–p_{i,j}}{d}–\frac{1}{Re{d}^2}(v_{i+1,j}+v_{i–1,j}+v_{i,j+1}+v_{i,j–1}–4v_{i,j}\left)\right]$

格子は正方格子とし、間隔を d と置きました。次回は前回の境界条件を考慮しつつ、上記の差分方程式を python + numpy で解くところまで行きたいと思います。

ここまでで２時間かかってしまった。