昨日の投稿で実装するべき数式を書き出しました。今日は python + numpy で実装したいと思います。
#! -*- coding: utf-8 -*-
import sys
import numpy as np
import matplotlib.pyplot as plt
# 二次元 cavity 問題の解法
class cavity2d:
def __init__(self, dt, nlattice, Re, u0):
self.dt = dt
self.nlattice = nlattice
self.d = 1 / nlattice
self.Re = 100
self.u0 = u0
self.t = 0.0
self.niter = 2000
self.maxerr = 0.01
# 物理量
self.p = np.zeros([nlattice + 2, nlattice + 2], dtype=np.float64)
self.u = np.zeros([nlattice + 2, nlattice + 3], dtype=np.float64)
self.v = np.zeros([nlattice + 3, nlattice + 2], dtype=np.float64)
# 補助量
self.large_d = np.zeros([nlattice, nlattice], dtype=np.float64)
self.p_rhs = np.zeros([nlattice, nlattice], dtype=np.float64)
self.p_lhs = np.zeros([nlattice, nlattice], dtype=np.float64)
self.u_rhs = np.zeros([nlattice - 1, nlattice - 1], dtype=np.float64)
self.v_rhs = np.zeros([nlattice - 1, nlattice - 1], dtype=np.float64)
self.ua = np.zeros([nlattice - 1, nlattice - 1], dtype=np.float64)
self.ub = np.zeros([nlattice, nlattice], dtype=np.float64)
self.uc = np.zeros([nlattice, nlattice], dtype=np.float64)
self.va = np.zeros([nlattice - 1, nlattice - 1], dtype=np.float64)
self.vb = np.zeros([nlattice, nlattice], dtype=np.float64)
self.vc = np.zeros([nlattice, nlattice], dtype=np.float64)
# 平均量の計算
def average(self, z, n, c):
return (z[2+c[0]:n+c[0], 2+c[1]:n+c[1]] \
+z[3+c[0]:n+1+c[0], 2+c[1]:n+c[1]] \
+z[2+c[0]:n+c[0], 3+c[1]:n+1+c[1]] \
+z[3+c[0]:n+1+c[0], 3+c[1]:n+1+c[1]]) / 4.0
# Laplace 演算子
def laplace(self, z, x_bd, y_bd):
return z[x_bd[0]+1:x_bd[1]+1,y_bd[0]:y_bd[1]] +z[x_bd[0]-1:x_bd[1]-1,y_bd[0]:y_bd[1]] +z[x_bd[0]:x_bd[1],y_bd[0]-1:y_bd[1]-1] +z[x_bd[0]:x_bd[1],y_bd[0]+1:y_bd[1]+1]
# 圧力の境界条件
def boundary_p(self):
# 辺 CD
self.p[self.nlattice+1, :] = self.p[self.nlattice, :] - (self.v[self.nlattice - 2, :] - 2.0 * self.v[self.nlattice - 1, :]) / self.d / self.Re
# 辺 DA
self.p[:, 0] = self.p[:, 1] + (self.u[:, 3] - 2.0 * self.u[:, 2]) / self.d / self.Re
# 辺 AB
self.p[0, :] = self.p[1, :] + (self.v[3, :] - 2.0 * self.v[2, :]) / self.d / self.Re
# 辺 BC
self.p[:, self.nlattice+1] = self.p[:, self.nlattice] - (self.u[:, self.nlattice - 2] - 2.0 * self.u[:, self.nlattice - 1]) / self.d / self.Re
# u, v の境界条件
def boundary_uv(self):
# 辺 CD
self.v[self.nlattice+2, :] = self.v[self.nlattice, :]
self.v[self.nlattice+1, :] = 0
self.u[self.nlattice+1, :] = self.u0 / 4.0 - self.u[self.nlattice, :]
# 辺 DA
self.u[:, 0] = self.u[:, 2]
self.u[:, 1] = 0
self.v[:, 0] = -self.v[:, 1]
# 辺 AB
self.v[0, :] = self.v[2, :]
self.v[1, :] = 0
self.u[0, :] = -self.u[1, :]
# 辺 BC
self.u[:, self.nlattice+2] = self.u[:, self.nlattice]
self.u[:, self.nlattice+1] = 0
self.v[:, self.nlattice+1] = -self.v[:, self.nlattice]
# 連続の式
def cont_eq(self):
self.large_d[:,:] = (self.v[2:self.nlattice+2,1:self.nlattice+1] - self.v[1:self.nlattice+1,1:self.nlattice+1] \
# ua, ub, va, vb の計算
def calc_uv(self):
self.ua[:,:] = self.average(self.u, self.nlattice + 1, (0, 0))
self.ub[:,:] = self.average(self.u, self.nlattice + 2, (-1, -1))
self.uc[:,:] = self.average(self.u, self.nlattice + 2, (-2, -1))
self.va[:,:] = self.average(self.v, self.nlattice + 1, (0, 0))
self.vb[:,:] = self.average(self.v, self.nlattice + 2, (-1, -1))
self.vc[:,:] = self.average(self.v, self.nlattice + 2, (-1, -2))
# 圧力右辺の計算 (poisson 項除く)
def calc_p_rhs(self):
self.p_rhs[:,:] = -self.d ** 2 / self.dt * self.large_d \
+(self.u[1:self.nlattice+1, 2:self.nlattice+2] - self.u[1:self.nlattice+1, 1:self.nlattice+1]) ** 2 \
+(self.v[2:self.nlattice+2, 1:self.nlattice+1] - self.v[1:self.nlattice+1, 1:self.nlattice+1]) ** 2 \
+2.0 * (self.ub[:,:] - self.uc[:,:]) * (self.vb[:,:] - self.vc[:,:])
# 圧力の poisson 方程式を Gauss 法で解く
def solve_p(self):
self.boundary_uv()
self.boundary_p()
self.calc_uv()
self.calc_p_rhs()
err = self.maxerr
for _ in range(self.niter):
self.p_lhs[:,:] = (self.laplace(self.p, (1, self.nlattice+1), (1, self.nlattice+1)) + self.p_rhs[:,:]) / 4.0
err = np.max(np.abs(self.p[1:self.nlattice+1,1:self.nlattice+1] - self.p_lhs[:,:]))
self.p[1:self.nlattice+1,1:self.nlattice+1] = self.p_lhs[:,:]
if err < self.maxerr:
break
if err >= self.maxerr:
print("{:.4f}: err not converged:".format(self.t), err)
# u,v を時間発展させる
def evolve_uv(self):
self.u_rhs[:,:] = self.u[2:self.nlattice+1,2:self.nlattice+1] * (self.u[2:self.nlattice+1, 3:self.nlattice+2] - self.u[2:self.nlattice+1, 1:self.nlattice+0]) / 2.0 / self.d \
+ self.va[:,:] * (self.v[3:self.nlattice+2, 2:self.nlattice+1] - self.v[1:self.nlattice+0, 2:self.nlattice+1]) / 2.0 / self.d \
+ (self.p[2:self.nlattice+1, 3:self.nlattice+2] - self.p[2:self.nlattice+1,2:self.nlattice+1]) / self.d \
- (self.laplace(self.u, (2, self.nlattice+1), (2, self.nlattice+1)) - 4.0 * self.u[2:self.nlattice+1,2:self.nlattice+1]) / (self.d ** 2) / self.Re
self.u_rhs[:,:] = self.u[2:self.nlattice+1,2:self.nlattice+1] - self.u_rhs[:,:] * self.dt
self.v_rhs[:,:] = self.v[2:self.nlattice+1,2:self.nlattice+1] * (self.v[3:self.nlattice+2,2:self.nlattice+1] - self.v[1:self.nlattice+0,2:self.nlattice+1]) / 2.0 / self.d \
+ self.ua[:,:] * (self.u[2:self.nlattice+1,3:self.nlattice+2] - self.u[2:self.nlattice+1,1:self.nlattice+0]) / 2.0 / self.d \
+ (self.p[3:self.nlattice+2, 2:self.nlattice+1] - self.p[2:self.nlattice+1,2:self.nlattice+1]) / self.d \
- (self.laplace(self.v, (2, self.nlattice+1), (2, self.nlattice+1)) - 4.0 * self.v[2:self.nlattice+1,2:self.nlattice+1]) / (self.d ** 2) / self.Re
self.v_rhs[:,:] = self.v[2:self.nlattice+1,2:self.nlattice+1] - self.v_rhs[:,:] * self.dt
# 計算結果を代入
self.u[2:self.nlattice+1, 2:self.nlattice+1] = self.u_rhs[:,:]
self.v[2:self.nlattice+1, 2:self.nlattice+1] = self.v_rhs[:,:]
self.t += self.dt
if __name__ == '__main__':
nlattice = 30
ntime = 35000
if len(sys.argv) > 1:
nlattice = int(sys.argv[1])
if len(sys.argv) > 2:
ntime = int(sys.argv[2])
c2d = cavity2d(dt = 0.001, nlattice=nlattice, Re = 100, u0 = 1.0)
for _ in range(ntime):
c2d.solve_p()
c2d.evolve_uv()
x, y = np.meshgrid(np.arange(0, nlattice + 1), np.arange(0, nlattice + 1))
u = c2d.u[1:nlattice+2,1:nlattice+2] * 15.0
v = c2d.v[1:nlattice+2,1:nlattice+2] * 15.0
pmin = np.min(np.abs(c2d.p))
pmax = np.max(np.abs(c2d.p) - pmin)
pcol = (np.abs(c2d.p) - pmin) / pmax
print(pcol)
plt.rc('font', size=22)
plt.xlim(0, nlattice)
plt.ylim(0, nlattice)
fig, ax = plt.subplots(figsize=(20, 10))
ax.imshow(pcol, origin='lower')
ax.quiver(x, y, u, v, units='xy', scale=1, color='black')
ax.grid()
plt.title('fluid velocities')
plt.savefig('cavity2d.png')
レイノルズ数は100固定としました。デフォルトでは流速は右方向に大きさ1、格子数は30、時間間隔は0.001で35000回計算します。Poisson 方程式の陰解法の収束誤差は0.01とします。
matplotlib を使い、結果を png ファイルに出力したものが以下となります。Core i7 13700KF で6秒ほど要しました。図では圧力をヒートマップにしていますが、分かり辛いです(泣)。
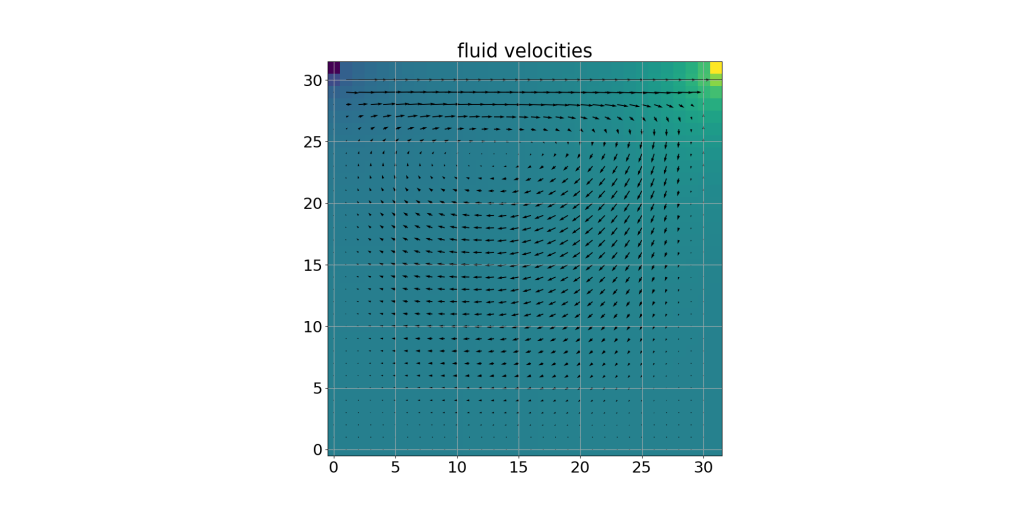
数値計算は昔から苦手でなかなかバグが取れないのですが、今回もご多分に漏れず、結果を取得するのに1日かかってしまいました。いくつか理由があるのですが、
- 数式の符号の間違いに気づきにくい
- 圧力と流速ベクトルで定義数が違う
- 境界条件の数が圧力と流速ベクトルとで異なる
- Numpy の二次元配列定義は x, y が逆になる
というようなことに中々気づきませんでした。
参考図書では10ページくらいで解説されていますが、実際に手を動かしてみると「この時はどうすればいいんだっけ??」という疑問が湧いてきて数式を味わい直すという楽しい(?)作業が必要になります。

コメントを残す